CAP 10 – Etablissement de la courbe Pn = f (V) à partir de mesures en vol
Le but est d’établir la courbe de puissance nécessaire au vol (Pn) en palier à partir des valeurs réelles de la pression d’admission (PA) et du régime moteur (RPM) correspondant aux différentes vitesses.
Rappelons que Pn dépend des caractéristiques géométriques et aérodynamiques de l’avion, de sa masse pendant le vol et de la masse volumique de l’air.
Le CAP 10 a été choisi car c’est un des rares appareils d’aéro-club disposant d’une hélice à calage fixe et d’un indicateur de pression d’admission. L’intérêt d’une hélice à calage fixe est la simplification dans l’évaluation de son rendement, le calage restant constant quelque soit la vitesse de l’avion, ce qui n’est pas le cas pour une hélice « à vitesse constante ». La connaissance des paramètres PA et RPM permet, à partir des données du motoriste, de préciser la puissance délivrée par le moteur (Pm).
La seule connaissance du régime moteur, ce qui est le cas d’une majorité d’appareils de faible puissance non équipés de mesure de la pression d’admission, ne permet pas à elle seule d’évaluer la puissance délivrée par celui-ci, même si elle donne une bonne idée de la forme de cette dernière en fonction de la vitesse. Ceci constitue une première approche pour montrer à l’élève-pilote la présence de ce minimum de puissance nécessaire au vol et de la vitesse associée.
La puissance en sortie d’hélice (Pu) est ensuite calculée à partit du rendement de l’hélice (ŋh). Ce dernier est fonction du » paramètre de fonctionnement de l’hélice J « , déterminé comme suit:
J = V / N.D, avec :
V : Vitesse d’avancement de l’hélice (vitesse avion)
D : diamètre de l’hélice
N : vitesse de rotation
On a : Pu = Pm . ŋh
En vol palier : Pn = Pu.
Caractéristiques du groupe motopropulseur du CAP 10 utilisé
- Moteur Lycoming AEIO 360 B2F, puissance nominale : 180 hp à 2700 t/mn.
- Hélice Hoffmann HO 29 HM-180-170 Diamètre: 1.80 m Calage à 0.75 R : 21°
Vol effectué
Le vol est effectué à une altitude de 1500′ QNH avec les conditions suivantes:
QNH = 1021 hPa Température dans la zone de vol = 24°C (MV air = 1.127 kg/m3)
M = 785 kg
Configuration lisse
Le principe est d’évoluer à différentes vitesses, en palier, entre la vitesse maximum de vol et la vitesse de décrochage (Vs), et de noter les couples PA / RPM associés.
Résultats
Le tableau suivant présente les résultats des mesures avec les étapes du calcul permettant d’obtenir les valeurs de Pu, et donc de Pn, correspondant aux différentes vitesses. La figure 1 présente la pression d’admission (PA) nécessaire en fonction de la vitesse;
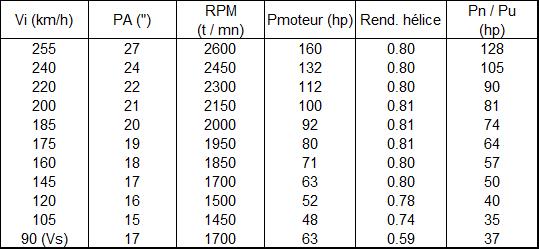
Note: la vitesse à prendre en compte pour le calcul du rendement d’hélice est la vitesse propre de l’appareil (Vp). En raison des conditions de pression et de température pendant le vol, et par souci de simplification, il est assimilé Vp = Vi, le but n’étant pas de calculer une relation exacte Pn = f(Vp) mais surtout de préciser la forme de celle-ci et l’ordre de grandeur des puissances rencontrées. Il en est de même pour la puissance moteur pour laquelle aucune correction de densité de l’air n’est effectuée (on considère Zp = 0 et T standard).
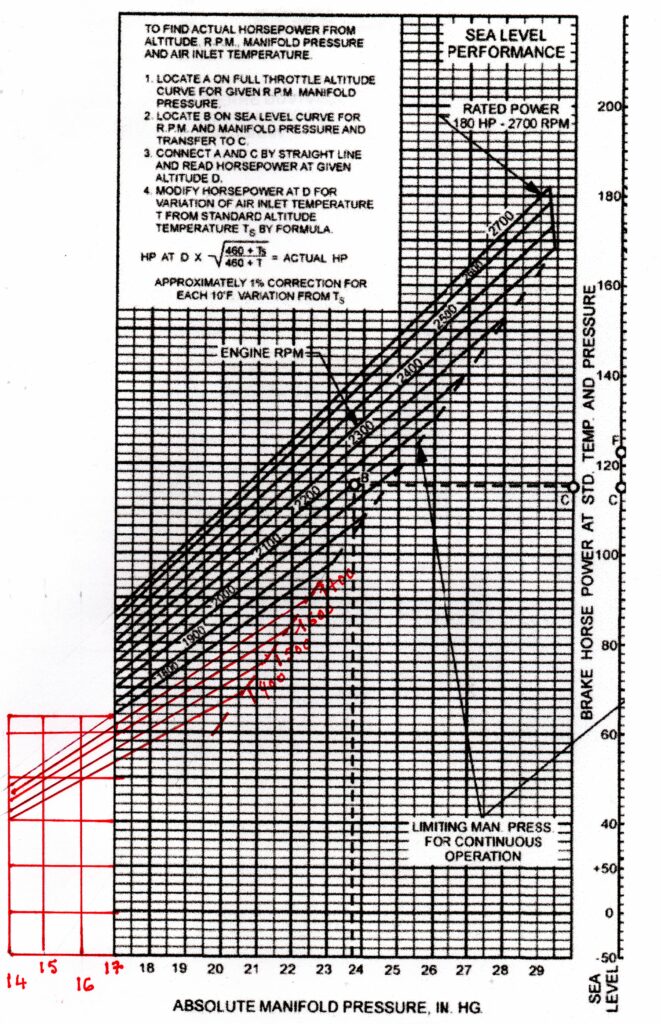
La puissance délivrée par le moteur (Pm) est déterminée à partir de l’abaque Lycoming en figure 2 ci-jointe.
Celui-ci n’indique pas de données inférieures à:
- 1800 t/mn pour le régime moteur,
- 17″ pour la pression d’admission
En conséquence il est effectué une extrapolation graphique, en rouge sur l’abaque, pour des valeurs de RPM jusqu’à 1400 t/mn et des valeurs de PA jusqu’à 14″.
Que les puristes jettent les premières pierres……..☺
Concernant le rendement de l’hélice, on utilise la courbe en figure 3 ci-dessous.
C’est le paramètre le plus critique pour la détermination de Pu / Pn, et le choix de la courbe J = V / N.D retenue montre une influence notable sur les valeurs de puissance obtenues.
On peut alors tracer la courbe Pn = f(Vi), représentée par la figure 4 ci-dessous.
Plus que la valeur absolue de Pn pour les différentes vitesses (qui comme signalé ci-dessus est influencée par le rendement hélice, non connu avec précision pour celle équipant ce CAP 10), c’est surtout sur la forme de cette courbe expérimentale que l’on doit s’arrêter.
Effectivement, l’allure de celle-ci présente des points similaires à celle de la courbe théorique que l’on peut établir à partir des caractéristiques d’un appareil, en particulier:
- pas de remontée verticale à l’approche de la vitesse de décrochage, tel que cela est trop souvent présenté,
- un minimum de la courbe correspondant à une vitesse très proche de la vitesse de décrochage, et donc non situé dans le milieu du domaine de vitesses de l’avion, là aussi, représentation régulièrement rencontrée.
Concernant ce minimum, il correspond dans ces mesures en vol à une vitesse d’environ 105 km/h (Vpmini). On retrouve une valeur très voisine de celle que l’on peut calculer à partir de la vitesse de finesse maximum (Vfmax) indiquée dans le manuel de vol du CAP 10, à savoir 140 km/h. Effectivement, la relation théorique entre ces 2 vitesses est Vpmini = 0,76 Vfmax.
Comparaison avec la courbe théorique
La courbe théorique correspondant aux conditions de ce vol peut être déterminée à partir de la relation suivante (établie ICI):
Pn = ½ . ρ . V3 . S . Cxp + 2 . (m. g)2 / ρ . V . S . π. ƛ .e
Les données maîtrisées sont les suivantes:
M = 785 kg, S = 10.85 m2, ƛ = 5.96, ρ = 1.127 kg/m3
L’incertitude réside sur les caractéristiques aérodynamiques du CAP 10, à savoir Cxp et e. La finesse maximum de l’avion indiquée dans le manuel de vol est de 10, ce qui est similaire à celle du DR 400. On peut donc supposer que ces 2 paramètres sont du même ordre de grandeur que ceux du DR 400.
La vitesse indiquée pour l’obtention de la finesse maximum est de 140 km/h (la masse correspondante n’est pas indiquée dans le manuel de vol).
Sur le plan théorique, la vitesse de finesse maximum peut être calculée comme suit (démonstration ICI):
V fmax = [ 4 . (m . g)2 / ρ2 . S2 . Cxp . π . ƛ . e ]1/4
Un couple de valeurs pour e et Cxp permettant de vérifier, à partir de cette formule, Vfmax = 140 km/h est e = 0.8 et Cxp = 0.04.
- e est choisi supérieur à la valeur utilisée pour le DR 400 (0.7) et qui vérifie les mesures en vol. On peut expliquer ceci (il n’est pas interdit d’oser…☺) par le fait que l’aile du CAP 10 est de forme semi-elliptique, ce qui contribue à diminuer la traînée induite et donc augmenter la valeur de e (effectivement, sur un plan théorique, une aile elliptique correspond à e = 1)
- Par conséquence, Cxp se trouve être légèrement supérieur au Cxp du DR 400, tel que déterminé à partir de mesures en vol (0.035).
A partir des valeurs, on peut tracer la courbe théorique Pn = f(V) et comparer ainsi avec celle obtenue expérimentalement, ce qui est présenté dans la figure 5 ci-dessous.