Formulaire de physique

Principales unités
Formules de base en mécanique
Note: certaines des grandeurs présentes sont dites « vectorielles » c’est-à-dire qu’elles sont caractérisées par leur amplitude et leur direction, telles force, moment, vitesse, accélération, quantité de mouvement. Par souci de simplification on ne considère dans ces formules que l’amplitude.
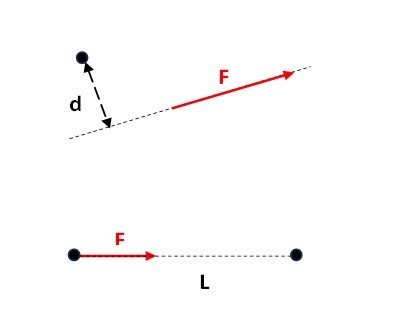
Moment d’une force (M)
Moment = force x distance par rapport à un point
M = F . d M en N.m
Travail d’une force (W)
Travail = force x déplacement
W = F . L W en joule avec F en N et L en m
Energie (E)
Définition : capacité d’un corps à effectuer un travail
E en joule
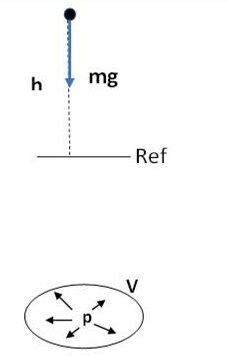
Types d’énergies mécaniques
- Energie potentielle E = m . g . h
m : masse en kg et h (hauteur/référence) en m
(m.g est le poids du corps en N) g = 9.81 m/s2
- Energie cinétique E = ½ m . v2
m : masse en kg et v (vitesse du corps ) en m/s
- Energie de pression E = p . V
P : pression en Pa et V (volume) en m3
Puissance (P)
Définition : énergie fournie par unité de temps
P = E / t P en watt E en joule et t en seconde
C’est aussi, puisque E ↔ W et W = F . L :
P = F . L/t = F . v (v = L/t)
Cas d’un système en rotation: P = C . ω avec C : couple en N.m et ω : vitesse de rotation en rad/s
Quantité de mouvement (p)
Définition: produit de la masse du corps par sa vitesse
p = m . v p en kg.m/s
Principe fondamental de la dynamique (en supposant ici masse = cte)
= la variation dans le temps de la quantité de mouvement p d’un corps de masse m et de vitesse v est égale à la somme des forces qui lui sont appliquées
Soit Σ F = dp/dt = m . dv/dt ou Σ F = m . a
a étant l’accélération en m/s2
Note : quand Σ F = 0, l’accélération a est nulle, donc la vitesse est constante (ou nulle).
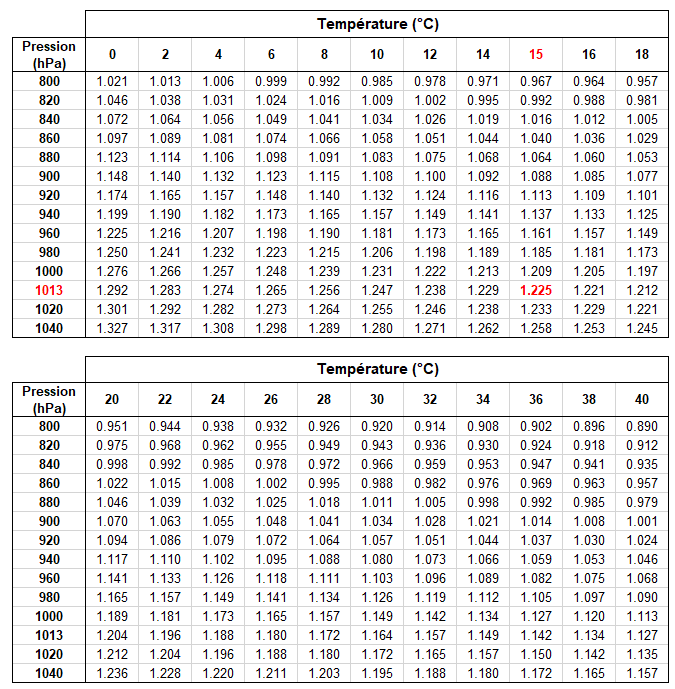
Calcul de la masse volumique de l’air
La masse volumique peut être calculée en appliquant la loi des gaz parfaits, l’air se comportant comme tel dans le domaine des températures et pressions rencontrées dans notre environnement.
Sa masse volumique, suivant les références, a pour valeur :
ρ = 1.292 kg/m3 dans les conditions « normales », à savoir P = 1013.25 hPa et T = 0°C (273.15 K)
ρ = 1.225 kg/m3 dans les conditions « standard » de l’atmosphère, à savoir P = 1013.25 hPa et T = 15°C (288.15 K)
En prenant cette dernière référence, la masse volumique en fonction de la pression et de la température est déterminée comme suit:
ρ = 1.225 . ( P / 1013) . 288 / (T + 273) avec P en hPa et T en °C
Le tableau suivant présente les valeurs de ρ pour des pressions rencontrées entre 0 et 5000 pieds et des températures de 0 à 40 °C.
Atmosphère standard
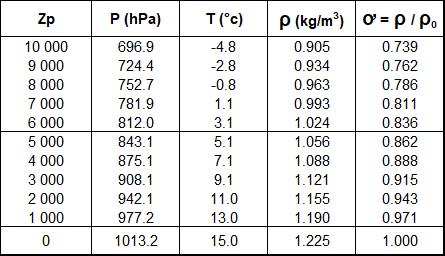
L’Atmosphère Standard Internationale (ISA en terminologie anglo-saxonne) est un modèle qui décrit une atmosphère théorique correspondant à une moyenne des atmosphères rencontrées dans les régions tempérées. Elle décrit les paramètres de pression, température, masse volumique, viscosité en fonction de l’altitude. Le tableau ci-dessous présente certaines de ces valeurs théoriques dans les basses couches.
Calcul de l’altitude-densité (AD)
Il est indiqué 3 méthodes d’évaluation de l’altitude-densité. Celles-ci considèrent un air sec ou faiblement humide.
1. Formule simplifiée
AD = AP + (T – Ts) x 120 avec:
AD en pieds
AP : Altitude pression de l’aérodrome (en pieds) = (1013 – QFE) x 28
T: température sur l’aérodrome en °C
Ts: température standard sur l’aérodrome en °C = 15 – 2 x AP / 1000
2. Calcul à partir de la masse volumique de l’air (ρ)
La masse volumique de l’air (ρ) est calculée comme suit:
ρ = 1.225 . ( P / 1013) . 288 / (T + 273) ρ en kg/m3
P: pression sur l’aérodrome (QFE) en hPa et T: température en °C
On détermine alors AD (en pieds) à partir de la formule approchée ci-dessous:
AD = – 8506 (ρ)3 + 38663 (ρ)2 – 84444 (ρ) + 61062
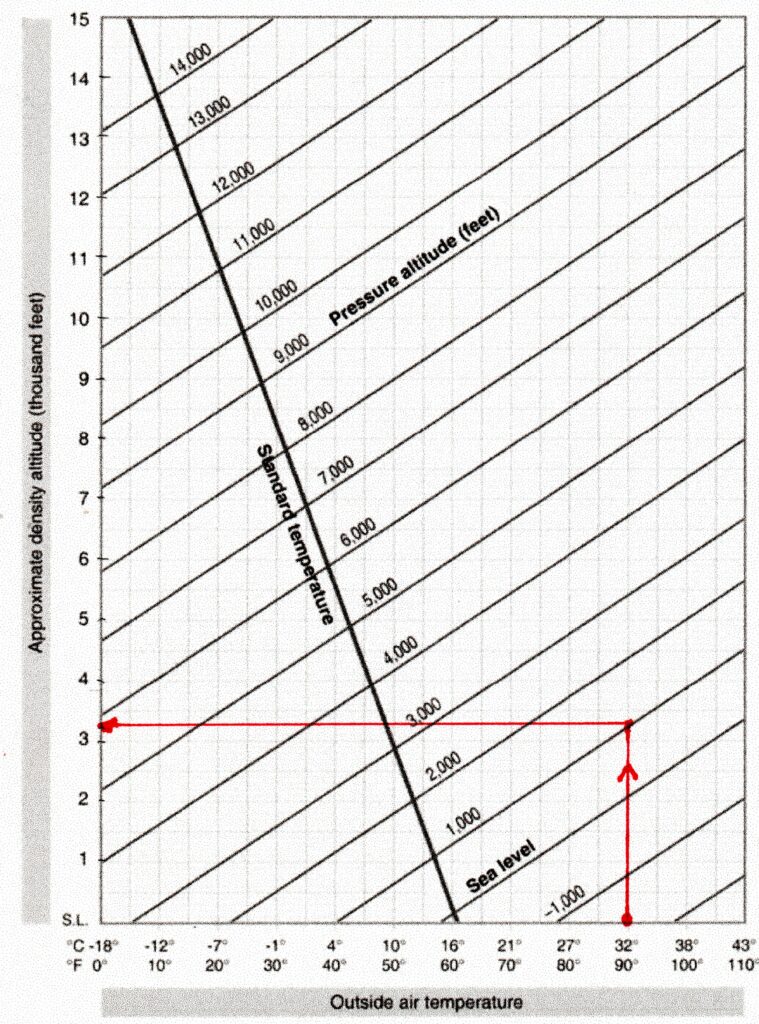
3. Utilisation d’abaque
La documentation technique en ce domaine présente plusieurs formes d’abaques, tel celui montré ci-contre, qui permettent une évaluation rapide de l’altitude-densité, après avoir préalablement calculé l’altitude-pression de l’aérodrome.
Exemple: calcul de l’AD pour les conditions suivantes:
QNH = 1013, altitude aérodrome = 1000 pieds, QFE = 977 hPa, T = 32°C
L’altitude-pression est 1000 pieds (puisque QNH = 1013).
A partir de la méthode 1 :
AD = 1000 + (32 – 13) x 120 = 3280 pieds
A partir de la méthode 2 :
ρ = 1.225 . ( 977 / 1013) . 288 / 305 = 1.116 kg/m3
AD = 3153 pieds
A partir de la méthode 3 :
L’abaque indique AD de l’ordre de 3200 pieds