Coefficient de pression (Cp) et de portance (Cz)
Définition du coefficient de pression Cp
Il est usuel de caractériser un profil d’aile à partir du coefficient de pression (Cp). Ce coefficient, comme le coefficient de frottement (Cf), est relatif à un point particulier de l’aile.
Il a pour valeur :
Cp = (P – P0) / q0 avec :
P = pression au point considéré
q0 = ½. ρ.V02 qui est la pression dynamique
V0 et P0 = respectivement vitesse et pression de l’air loin de l’aile
Ce coefficient est donc le rapport de l’écart de pression (par rapport à la pression atmosphérique) en un point de l’aile sur la pression dynamique maximum que l’on peut rencontrer sur l’aile, à savoir le point d’arrêt situé au niveau du bord d’attaque. La relation précédente s’exprime aussi, en appliquant la loi de Bernoulli:
Cp = (½. ρ.V02 – ½. ρ.V2) / ½. ρ.V02
V étant la vitesse de l’air au point considéré.
Ce qui donne finalement :
Cp = 1 – (V/V0)2
Cp est un nombre sans dimension, caractéristique du profil.
Exemple: profil NACA 2412
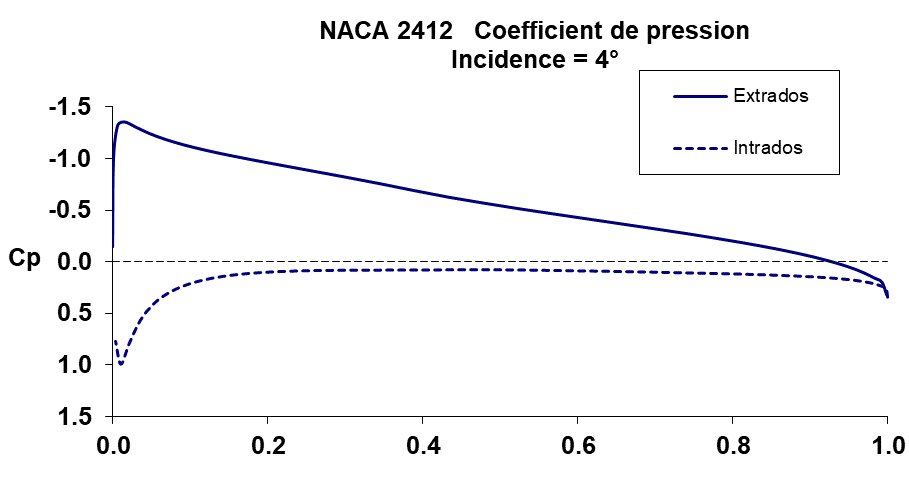
La figure ci-dessous présente la variation de Cp en fonction de la distance (longueur de la corde de profil c = 1) par rapport au bord d’attaque, pour une incidence de 4°.
On présente l’axe des ordonnées en valeurs inversées et on remarque évidemment que l’allure des courbes est similaire à celles représentant le champ de pression.
- Quand V < V0, c’est-à-dire quand on est en présence d’une surpression, Cp est > 0. C’est le cas ici de l’intrados.
- Quand V > V0, c’est-à-dire quand on est en présence d’une dépression, Cp est < 0. C’est le cas ici de l’extrados.
- Quand V = 0, c’est le point d’arrêt, alors Cp = 1
- Quand V = V0, on a Cp = 0
Coefficient de portance Cz
De façon simplifiée, on peut définir un coefficient de pression moyen pour l’extrados (Cpme) et l’intrados (Cpmi), calculé comme suit, avec c variant de 0 à 1:
Cpme = ∫c Cpe(x).dx ( ∫ = somme sur la longueur x = c)
Cpmi = ∫c Cpi(x).dx .
On définit alors le coefficient de portance de l’aile: Cz = Cpmi – Cpme
Cpmi et – Cpme sont respectivement les coefficient de portance de l’intrados (Czi) et coefficient de portance de l’extrados (Cze).
Exemple: profil NACA 2412
Pour une incidence de 4°, les valeurs sont les suivantes:
Cpme = – 0.57
Cpmi = 0.16
D’où Cz = Czi + Cze = 0.16 + 0.57 = 0,73

Influence de la courbure sur le coefficient de portance
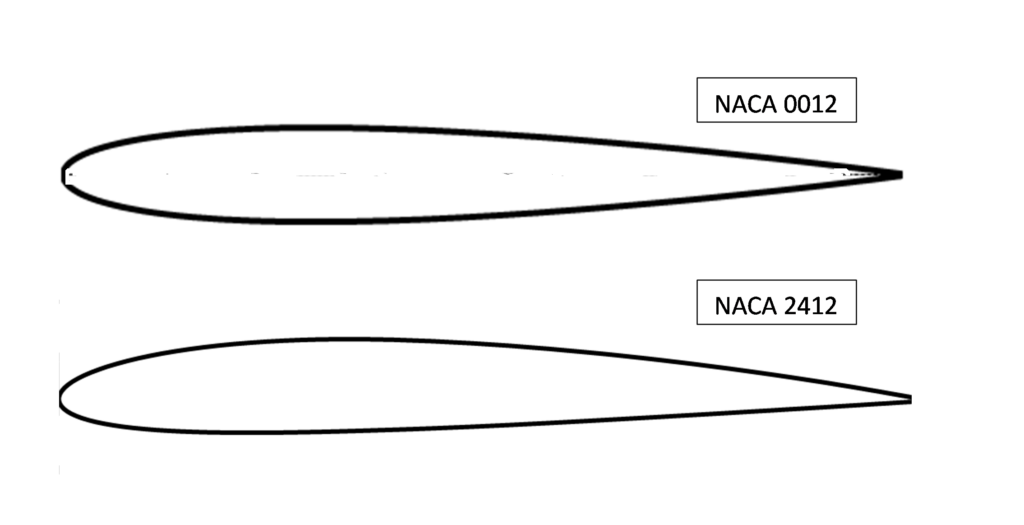
Toutes chose égales par ailleurs, la courbure de l’aile permet d’augmenter les performances de portance. A titre d’exemple, ci-dessous la valeur du Cz en fonction de l’incidence pour les profils NACA 0012 et NACA 2412. Ces profils ont la même épaisseur relative (12 %). Le profil NACA 0012 est symétrique (courbure = 0), le profil NACA 2412 présente une courbure de 2 %.
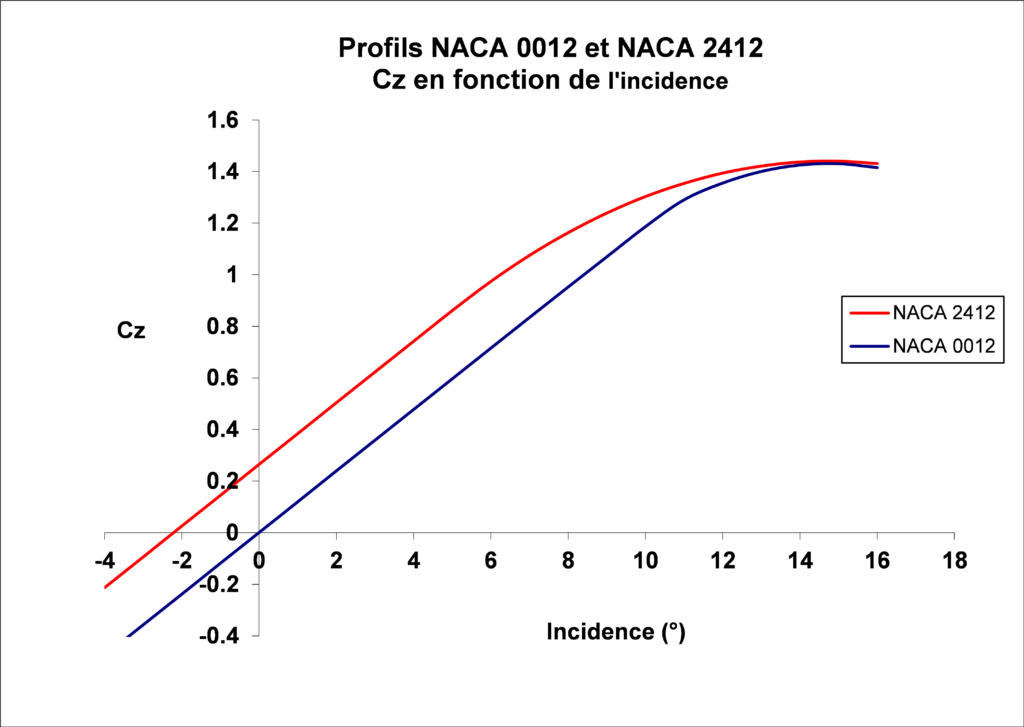
Pour une même incidence, NACA 2412 montre un Cz supérieur à NACA 0012. La valeur Cz = 0 (incidence de portance nulle) est obtenue pour:
- NACA 0012 : incidence = 0 °
- NACA 2412 : incidence = – 2.2 °
De façon générale, dans sa partie linéaire, le coefficient de portance Cz peut être estimé par la formule suivante :
Cz ≈ 2 . π . (1 + ε) . (α-α0) avec
ε = coefficient fonction de l’épaisseur. Pour les profils minces, on considère ε = 0
α = incidence (en radians)
α0 = incidence de portance nulle (en radians). Celle ci diminue quand la courbure du profil augmente
Note : cette relation considère un fluide parfait, c’est-à-dire non visqueux. En réalité, l’expérimentation révèle, qu’en raison des phénomènes de viscosité, la pente de cette courbe Cz = f(α) est plus faible que dans cette théorie du fluide parfait.