Relation entre Vfmax et Vpmini
Cohérence des courbes X = f(V) et Pn = f(V)
Les courbes de traînée aérodynamique totale X= f(V) et de puissance nécessaire au vol en palier Pn = f(V) doivent être cohérentes entre elles lors de leur présentation, en particulier la position de leurs minimums respectifs, à savoir:
- la vitesse de finesse maximum Vfmax, correspondant au minimum de la courbe de traînée (X)
- la vitesse Vpmini, correspondant au minimum de la courbe de puissance nécessaire (Pn)
Rappel (voir ICI) : les équations de ces courbes sont :
- pour la trainée: X = ½ . ρ . V2 . S . Cxp + 2 . (m. g)2 / ρ . V2 . S . π . ƛ . e
- pour la puissance nécessaire: Pn = ½ . ρ . V3 . S . Cxp + 2 . (m. g)2 / ρ . V . S . π . ƛ . e
Relation entre Vfmax et Vpmini
Pour simplifier, on écrit X = A .V2 + B / V2 et Pn = A . V3 + B / V dans lesquelles:
A = ½ . ρ . S . Cxp et B = 2 . (m. g)2 / ρ . S . π . ƛ . e
Calcul de Vfmax, correspondant au minimum de la courbe X = f(V)
X est minimum quand la dérivée par rapport à V est = 0
→ dX / dV = 2. A . V – 2 .B / V3 = 0 soit 2. A . V = 2 . B / V3 donc Vfmax4 = B / A
Calcul de Vpmini, correspondant au minimum de la courbe Pn = f(V)
Pn est minimum quand la dérivée par rapport à V est = 0
→ dPn / dV = 3. A . V2 – B / V2 = 0 soit 3. A . V2 = B / V2 donc Vpmini4 = 1/3 . B / A
On a alors: Vpmini4 = 1/3 . Vfmax4 soit Vpmini = (1/3)1/4 . Vfmax
Ce qui donne la relation simplifiée : Vpmini = 0.76 Vfmax
Exemple
On trace ci-dessous les courbes de traînée et de puissance nécessaire pour l’avion (fictif) dont les caractéristiques sont les suivantes:
m = 1200 kg, S = 15 m2, ƛ = 5.5, e = 0.7, Cxp = 0.025. et ρ = 1.225 kg/m3
Vs = 110 km/h, Vmax = 280 km/h
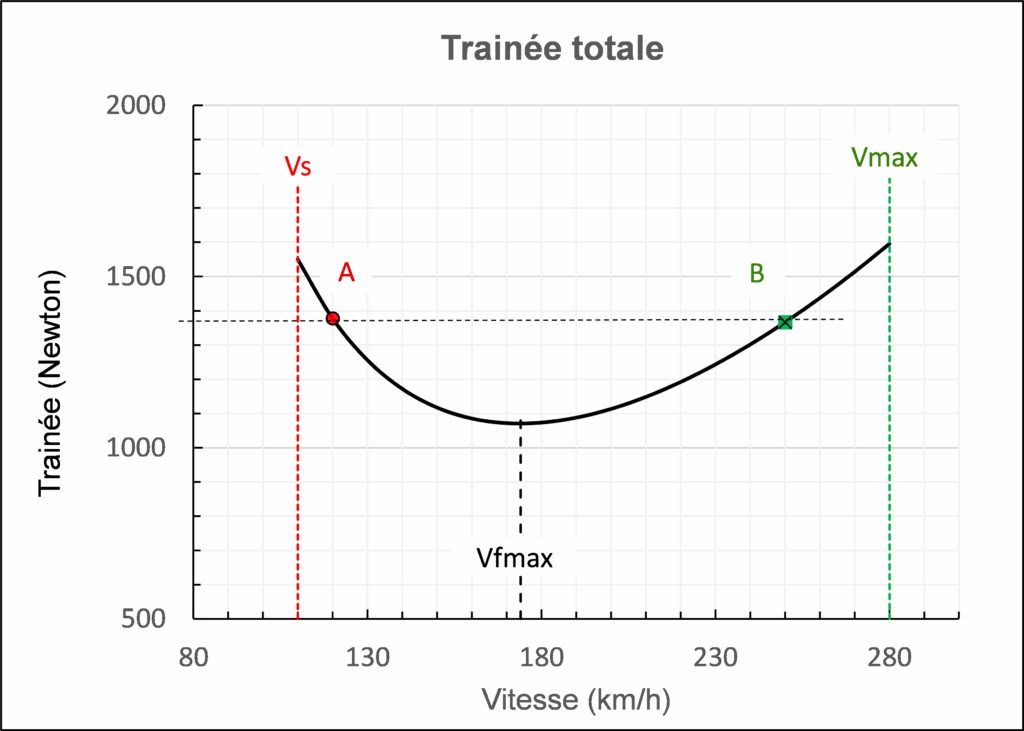
La courbe de traînée X = f(V) est présentée sur la figure 1.
Le minimum se produit pour Vfmax = 174 km/h.
Les points A et B correspondent à 2 cas de vol, respectivement pour V = 120 km/h et 250 km/h, présentant une même traînée, de l’ordre de 1380 N.
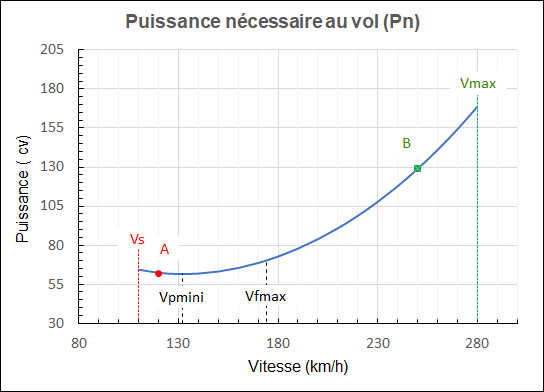
La courbe de puissance nécessaire au vol Pn = f(V) est présentée sur la figure 2.
Le minimum se produit pour Vpmini = 132 km/h.
On retrouve Vpmini = 0.76 . Vfmax.
Les points A et B correspondant aux 2 cas de vol à traînées identiques sont reportés sur la courbe Pn
Note1
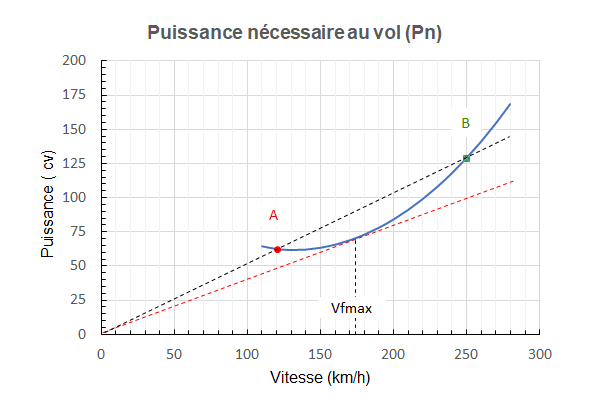
En prenant (0,0) comme origine pour les axes Puissance et Vitesse, on obtient le graphique en figure 3 ci-dessous.
- la droite partant de l’origine et tangente à la courbe indique le point de Vfmax (pointillé rouge) : rapport Pn / V minimum
- la droite reliant les 2 points A et B correspondant à une même valeur de traînée X(A) = X(B) passe par l’origine du graphique: Pn(A) / V(A) = Pn(B) / V(B)
Note 2
A la vitesse Vpmini, Traînée induite = 3 x Traînée parasite.
Démonstration:
La traînée totale peut être exprimée comme indiqué plus haut : X = A .V2 + B / V2 où A .V2 = trainée parasite (Xp) et B / V2 = traînée induite (Xi).
Le rapport Trainée induite / Traînée parasite vaut donc Xi /Xp = B / A .V4. Comme calculé plus haut, Vpmini4 = 1/3 . B / A.
Par conséquent, à cette vitesse, Xi /Xp = B / A . (1/3 . B / A) ou Xi /Xp =3 ou Xi = 3. Xp
En d’autres termes, à Vpmini, la traînée induite représente 75 % de la traînée totale.