Décollage – Accélération pendant la phase de roulage
Etat des forces en présence
Pendant la phase de roulage au sol après la mise en puissance, les forces en présence sont les suivantes:
- poids de l’avion : P = mg. Cette force reste constante.
- traction moteur : Tm. Après la mise en puissance (= plein gaz), celle-ci va évoluer au fur et à mesure de la prise de vitesse de l’avion sur la piste.
- portance aérodynamique : Z. Initialement nulle au moment de la mise en puissance, elle augmente avec la vitesse.
- trainée aérodynamique Xa. Initialement nulle au moment de la mise en puissance, elle augmente avec la vitesse.
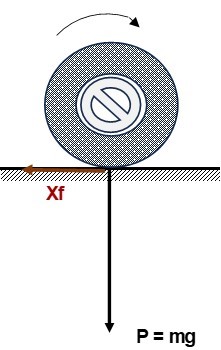
- trainée de friction due au roulement : Xf. Celle-ci est la conséquence des forces de frottement dit « solide » résultant du contact des pneus avec le sol.
Cette force de friction est proportionnelle à la force d’appui sur le sol. Dans le cas ou cette dernière est uniquement le poids du véhicule (P = mg), la traînée de friction s’exprime comme suit :
Xf = Cf.mg
Cf est le coefficient de frottement. Il est de l’ordre de 0.01 à 0.02 pour un contact sur un sol dur, sec.
Dans le cas particulier de l’avion au roulage, la portance Z, développée au fur et à mesure que la vitesse augmente, diminue la force d’appui au sol que constituait initialement le poids P. La traînée de friction s’exprime alors comme suit:
Xf = Cf.(mg – Z)
→ La traînée de friction diminue donc quand la vitesse de l’avion augmente.
Les figures suivantes présentent l’état des forces en début et en fin de roulage (avant la rotation).
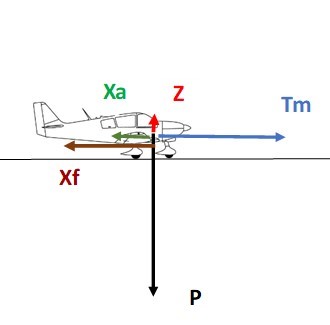
En début de roulage, après la mise en puissance progressive :
Xa est minimum
Z est minimum
→ Xf = Cf.(mg-Z) est maximum
Tm > (Xa + Xf) donc l’avion accélère
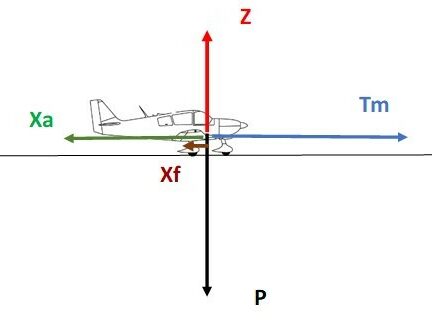
En fin de roulage, juste avant la rotation:
Xa a augmenté
Z a augmenté
→ Xf a diminué
Tm a augmenté
On a toujours Tm > (Xa + Xf)
Accélération pendant le roulage
L’accélération Γ est reliée aux différentes forces par le principe fondamental de la dynamique: Σ Forces = m . Γ. Sur une piste de pente γm, , la relation générale est:
Tm ± mgsin(γm) – Xa – Cf.[mgcos(γm) – Z] = m . Γ
Tm = traction due au GMP (sortie hélice)
± mgsin(γm) : composante du poids sur la trajectoire, agissant en traction (+) dans le cas où le décollage se fait dans le sens descendant, ou en traînée (–) dans le cas contraire (= 0 si γm = 0)
Xa : traînée aérodynamique (détail ICI)
Cf : coefficient de frottement pneu / sol
mgcos(γm) : composante du poids perpendiculaire au sol (= mg si γm = 0)
Z : portance (= ½ . ρ . V2 . S . Cz). Cz est inchangé pendant la phase de roulage au sol si l’on suppose que l’assiette de l’avion reste constante jusqu’à la rotation; il dépend de l’angle de calage de l’aile.
Dans le cas où la piste est horizontale (γm = 0), la relation s’exprime comme suit:
Tm – Xa – Cf.(mg- Z) = m . Γ
Exemple: enregistrement de la vitesse et de la distance parcourue lors d’un décollage
La figure 4 représente l’évolution de la vitesse et la distance parcourue depuis la mise en puissance d’un DR 400 2+2 au décollage avec les conditions suivantes:
Masse = 795 kg
Piste horizontale, QFE = 1026 hPa, T = 2°C, vent nul
Volets 1, mise en puissance sur frein
Vitesse de rotation : Vi = 100 km/h
Note: les vitesses / sol ainsi que la distance parcourue ont été enregistrées avec un logger GPS (pas : 1 s). Compte-tenu de l’absence de vent, on a Vi = V/sol.
L’accélération représente la pente de la courbe V = f(temps). Elle n’est pas constante, elle diminue légèrement au fur et à mesure de l’avancement de l’avion sur la piste.
La cause en est la diminution progressive de l’écart Tm – (Xa +Xf). La trainée de friction de roulement Xf diminue mais la traînée aérodynamique Xa augmente avec la vitesse.
Concernant la distance de roulement, celle-ci augmente de façon quasi parabolique similairement à celle d’un mouvement uniformément accéléré dont la loi est de la forme D = 1/2 . Γ . t2. Mais ici, Γ n’est pas constante, même si sa variation reste faible sur cette distance de roulage avant rotation.
Modélisation du décollage
On tente ici une modélisation du décollage tel qu’enregistré au-dessus, à savoir l’évaluation théorique des relations V = f(t) et DR = f(t).
L’accélération pendant le roulage ( Γ) à partir de la mise en puissance est définie par la relation ci-dessous:
Tm – Xa – Xf = m . Γ avec :
Tm = traction due au GMP (sortie hélice)
Xa : traînée aérodynamique = traînée parasite + traînée induite
Xf : traînée de frottement pneu / sol
De façon détaillée, on peut écrire:
Tm – ½ . ρ . V2 . S . (Cxp + Cz2/ π ƛ e) – Cf . (m . g – ½ . ρ . V2 . S . Cz) = m . Γ
Cz peut être évalué à partir de la relation : Cz ≈ 2 . π . (αc – α0) avec αc = angle de calage de l’aile et α0 = incidence de portance nulle du profil d’aile (on suppose que la portance Z de l’avion, et donc Cz, est liée uniquement à l’aile).
Comme indiqué plus, haut, on suppose Cz constant pendant toute la phase de roulage.
La principale inconnue est la traction moteur. A partir d’une mise en puissance sur frein, on peut évaluer la traction initiale, en statique. Mais après le lâché des freins et au cours du roulage, celle-ci va évoluer suivant les caractéristiques du moteur (relation entre la puissance de sortie et la vitesse de rotation) et de l’hélice (évolution du rendement en fonction de la vitesse).
Pour la traction d’hélice « statique » (à V = 0) , on peut estimer l’ordre de grandeur à partir de la relation suivante:
T = 9.187 10-12 . (RPM)2 . D4 . ρ
T en newton, RPM en t/mn, D (diamètre de l’hélice) en pouces, ρ en kg/m3 (Source: Static Thrust Measurement for Propeller-driven Light Aircraft – 2012)
Pour le vol considéré, les données sont:
RPM = 2250 t/mn (valeur constatée avant lâché des freins), D = 72″, ρ = 1.3 kg/m3 (pour QFE = 1026 hPa et T = 2°C), ce qui donne T = 1625 N
Résolution de V = f(t) et DR = f(t) par méthode numérique
Le principe est un calcul pas à pas (∆t = 1 seconde), en procédant comme suit :
- A t = 0, calcul de Γ0 = (Tm0 – Xf0) / m (Xa0 = 0 car V0 = 0)
- A t = 1, calcul de V1 = V0 + Γ0 . Δ t puis Xa1 et Xf1 (à partir de V1) puis Γ1 = (Tm0 – Xa1 – Xf1) / m et DR1 = V1 . Δ t
- A t = 2, calcul de V2 = V1 + Γ1 . Δ t puis Xa2 et Xf2 (à partir de V2) puis Γ2 = (Tm0 – Xa2 – Xf2) / m et DR2 = V2 . Δ t + DR1
- etc…
On suppose que la traction moteur ne varie pas pendant le roulage. Faute de grives, on mange des merles……..🙂
Les données sont les suivantes:
m = 795 kg, ρ = 1.3 kg/m3, S = 13.6 m2, ƛ = 5.35, e = 0.7, Cxp = 0.040, αc = 2.5°, α0 = – 3° (valeur estimée pour le profil NACA 43013.5 équipant le DR 400), Cf = 0.015
Les courbes suivantes sont obtenues en prenant Tm = 1500 N, valeur considérée constante durant la phase de roulage et qui permet la meilleure corrélation entre les valeurs enregistrées et celles obtenues par le calcul.