Profil d’aile de Joukowsky
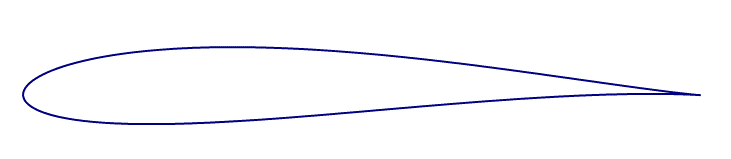
Ce profil d’aile est obtenu en transformant les points d’un cercle dans un repère orthonormé (X,Y) suivant la formule suivante:
p = Z + c2/Z
dans laquelle Z est le nombre complexe (réelle + imaginaire) représentant les coordonnées des points du cercle et c une constante (réelle). Cette transformation est appelée « Transformation de Joukowsky « .
Elle fut utilisée dans le passé pour le calcul des écoulements autour des profils d’aile. De nos jours, elle est souvent présente dans les modèles de simulation à but pédagogique.
Coordonnées du point-image après transformation
Dans le repère d’origine, la variable complexe peut être représentée en coordonnées cartésiennes ou polaires :
Z = x + iy, avec x et y les coordonnées cartésiennes
ou
Z = R eiθ = R (cos θ + i sin θ),
R et θ étant les coordonnées polaires
On a alors :
x = R cos θ et y = R sin θ
et R = (x2 + y2)1/2

En appliquant la transformation, on a :
p = R eiθ + c2 / [R eiθ] = R eiθ + [c2 / R] e-iθ = R (cos θ + i sin θ) + c2/R (cos θ – i sin θ)
p = (R + c2/R) cos θ + i (R – c2/R) sin θ
Comme p = X + iY , les coordonnées du point-image après transformation sont donc :
X = x + (c2/R) cos θ
Y = y – (c2/R) sin θ
Ce qui peut être représenté sur le graphe ci-contre →
En éliminant R et θ, on peut écrire :
X = x + c2 x / (x2 + y2)
Y = y – c2 y / (x2 + y2)

Transformée des points d’un cercle
En transformant un cercle passant systématiquement par le point d’abscisse (c,0), qui constitue un point fixe, et en faisant varier la position du centre du cercle, on obtient des profils d’aile dont le bord de fuite est toujours le point d’abscisse (2c,0).
L’épaisseur relative augmente quand le centre du cercle se déplace vers les X négatifs ou positifs.
La courbure relative augmente quand le centre du cercle se déplace vers les Y positifs ou négatifs.
Les graphiques ci-après représentent les formes de profil obtenues suivant la position du centre du cercle. On a considéré ici c = 1.
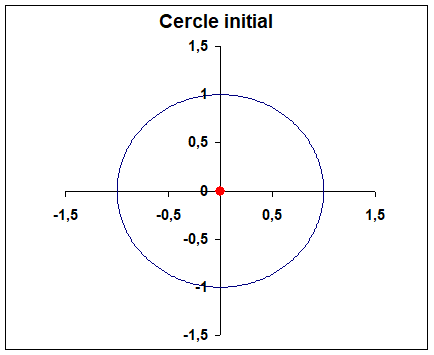
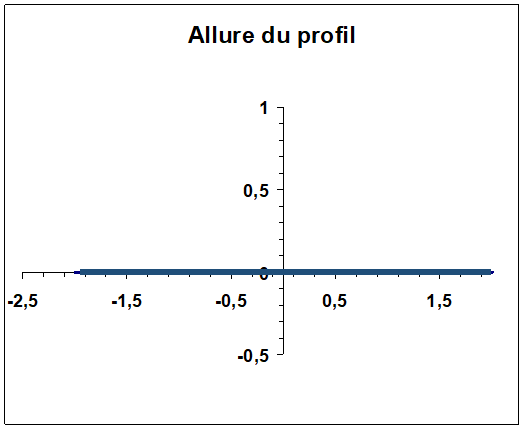
Centre du cercle à (0, 0) : la transformée est une plaque
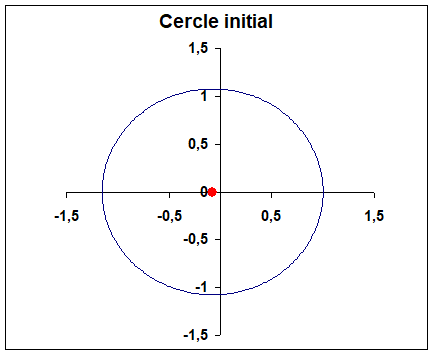
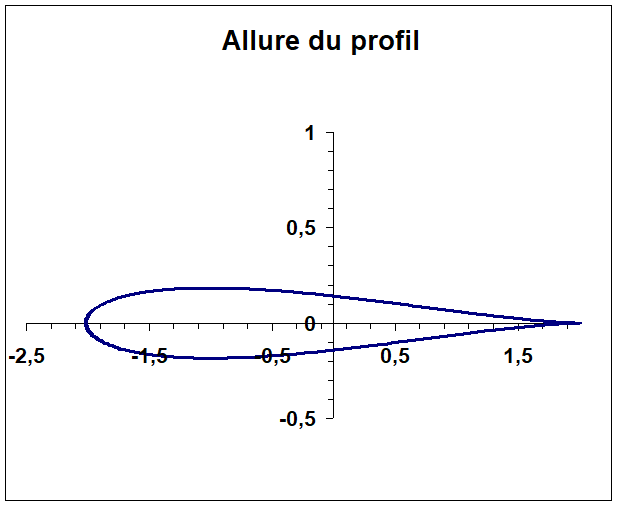
Centre du cercle à (-0,1, 0) : la transformée est un profil symétrique (courbure nulle)
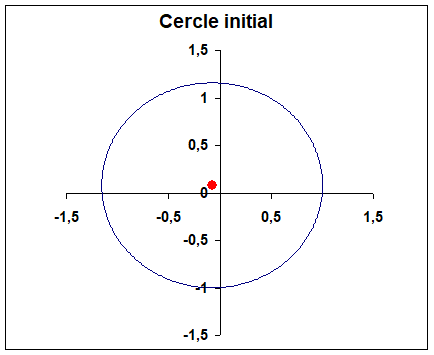
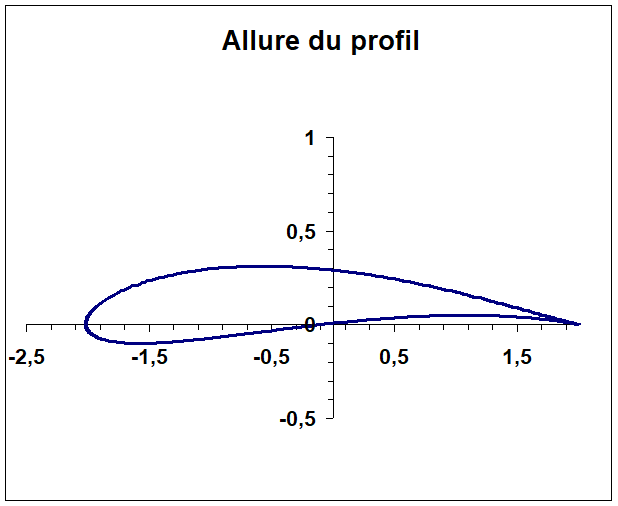
Centre du cercle à (-0,1, 0,1) : la transformée est un profil dissymétrique (courbure non nulle)