Loi de conservation de l’énergie
Une des lois fondamentales de la mécanique des fluides est la conservation de l’énergie. Elle exprime le fait que l’énergie totale d’une particule de fluide (gaz, liquide) reste constante lors de son déplacement, sous réserve qu’il n’y ait pas de perte d’énergie par frottement du fluide avec une surface ou par frottement des particules de fluides entre elles, en raison de la viscosité.
Pour un gaz, on peut négliger, dans les domaines des basses pressions, l’effet de la viscosité et assimiler alors ce gaz à un fluide « parfait ». Pour les liquides, ceci n’est pas possible et l’écoulement d’un liquide dans une installation (canalisation par exemple) se fait en perdant de l’énergie de façon d’autant plus accentuée que la viscosité est forte. Ces pertes d’énergie sont souvent appelées « pertes de charge ».
Considérons une particule d’air en mouvement, de masse m et de volume v. Son énergie totale est :
E = Et + P.v + m.g.h + ½.m.V2 avec :
Et : énergie thermique (fonction de la température)
P.v : énergie de pression, P étant la pression à laquelle est soumise cette particule de volume v
m.g.h : énergie potentielle, h étant la hauteur par rapport à un niveau de référence, g l’accélération de la pesanteur (g = 9,81 m/s2)
½.m.V2: énergie cinétique, V étant la vitesse de la particule
Dans son déplacement suivant le circuit représenté dans la figure ci-dessous, l’énergie de la particule reste constante.

On a E1 = E2 = E3, et par conséquent :
Et1 + P1.v + m.g.H1 + ½.m.V12 = Et2 + P2.v + m.g.H2 + ½.m.V22
= Et3 + P3.v + m.g.H3 + ½.m.V32
Sachant que m = ρ.v (ρ = masse volumique), et si on suppose une particule de volume unitaire (v = 1), on peut écrire :
E = Et + P + ρ.g.h + ½. ρ.V2 = constante
Application à l’aile en soufflerie
Supposons maintenant une particule d’air, circulant autour d’un profil d’aile entre les positions 0 et 1, tel que représenté sur la figure ci-dessous.
Entre la position initiale (0) et la position 1, on peut supposer avec une bonne approximation que :
- l’énergie thermique est restée constante (pas d’échange de chaleur avec l’aile ou avec les autres particules d’air)
- la différence d’énergie potentielle est négligeable, l’écoulement se faisant quasiment à niveau constant et la masse volumique de l’air étant faible
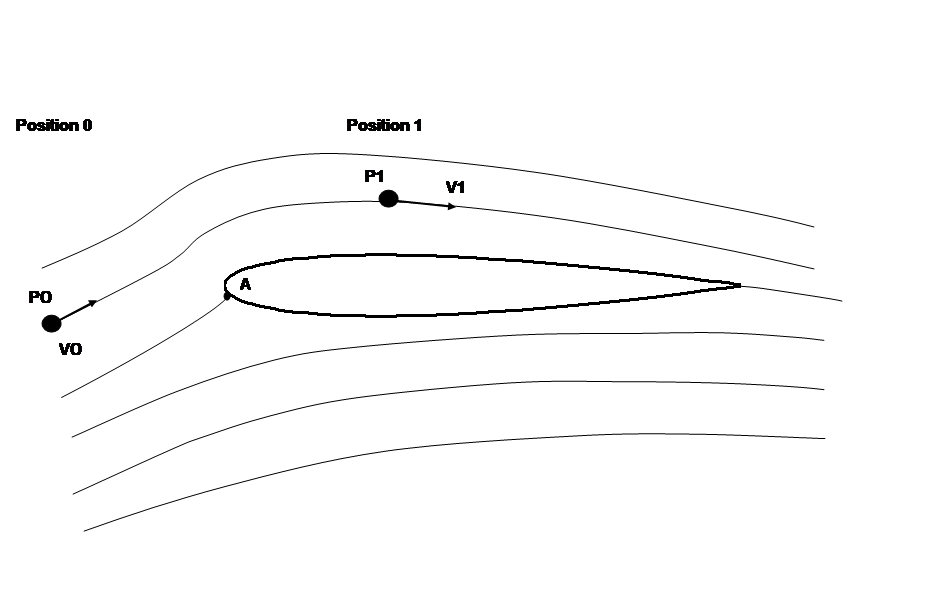
De plus, en raison des faibles vitesses induisant des variations de pression faibles (quelques %), on suppose que la masse volumique reste constante entre la position 0 et la position 1.
On peut alors écrire : P0 + ½. ρ.V02 = P1 + ½. ρ.V12
Cette relation est plus connue sous l’appellation loi (ou théorème, ou principe) de Bernoulli.
Le terme ½. ρ.V2 est appelé pression dynamique.
La somme correspondant à la pression statique + la pression dynamique P + ½. ρ.V2 est appelée pression totale.
On peut donc, à partir de la connaissance du profil de vitesse calculer la pression statique comme suit :
P1 = P0 + ½.ρ.(V02 – V12)
Au point A, qui est un point d’arrêt, la vitesse est nulle. La pression qui y règne est donc maximum et a pour valeur :
P (A) = P0 + ½. ρ.V02
Précautions : cette relation simplifiée entre pression et vitesse ne peut être appliquée qu’avec les réserves suivantes :
- cela concerne une même particule circulant sur une même ligne de courant. Elle n’est pas valable pour des particules différentes situées sur des lignes de courants différentes
- la viscosité est négligeable
- la variation de masse volumique est négligeable. Cette approximation est valable dans le cas des vitesses faibles rencontrées en aviation légère, et malgré le fait que l’air est un fluide compressible. En d’autres termes, les changements de pressions sont faibles au regard de la pression totale.