Le phénomène de portance

Personne ne découvrira ici que ce qui permet à tout aéronef de tenir en l’air est la conséquence de l’apparition, lorsque cet aéronef se déplace dans ce milieu, d’une force, appelée portance et qui, dirigée vers le haut, va s’opposer à celle inhérente à tout corps pesant et orientée vers le bas, plus communément désignée le poids. Tout pilote est au fait de ce principe élémentaire de la physique, qui est présenté dès les premières pages d’un quelconque manuel d’apprentissage au pilotage.
Les conditions qui conduisent à l’apparition de cette intrigante force de portance font par contre l’objet de beaucoup moins de clarté dans ces mêmes ouvrages. Le phénomène de portance, dans le cas qui nous concerne ici à savoir une portance « aérodynamique », est loin d’être simple. Toute opération de vulgarisation, évidemment nécessaire dans ces livres de cours, s’accompagne bien sûr d’omission de certains phénomènes, mais aussi parfois d’imprécisions notables, et plus grave d’affirmations complètement erronées.
Certaines incompréhensions ou interprétations inexactes proviennent du fait que, lors de l’explication du phénomène de portance, la démonstration est basée sur l’hypothèse « aile fixe au contact de l’air en mouvement autour du profil ». Ce concept est tout à fait adapté, c’est sur ce principe que l’on étudie les profils d’aile en soufflerie. Mais en présentant les choses de cette façon, on occulte certains phénomènes qui se passent dans la réalité autour de l’aile quand celle-ci se meut dans un fluide immobile. Ceci peut conduire à donner une interprétation erronée, principalement sur ce qui se rapporte au trajet de l’air et de son profil de vitesse autour de l’aile.
Pour cette raison, la présentation du phénomène à partir de l’aile se déplaçant dans un l’air immobile peut permettre d’éviter de tomber dans certains pièges .
Déplacement d’une plaque plane
Considérons au départ un profil beaucoup plus sommaire qu’une aile, à savoir une plaque plane, d’épaisseur négligeable. Sa vitesse (V) est représentée par son vecteur vitesse. L’angle que fait la plaque par rapport à son vecteur vitesse (V) est appelé incidence. Le bord avant de la plaque (point A) est appelé bord d’attaque, la partie arrière (point F) est désignée bord de fuite
Avec une incidence nulle: dans la figure 1 ci-dessous, on représente l’air par un ensemble de particules (ou molécules) schématisées par des points noirs. Un observateur situé sur le sol voit ces particules d’air immobiles (on supposera dans toutes les expériences qu’il n’y a pas de vent… !). Quand l’observateur voit passer la plaque devant lui, il ne perçoit aucune agitation des particules d’air. La plaque, bien qu’en mouvement, ne déplace pas d’air en raison de son épaisseur supposée nulle et de son incidence égale à zéro. Pour simplifier, on oubliera l’effet d’entraînement de l’air au contact de la surface dû à la très faible viscosité (couche limite).
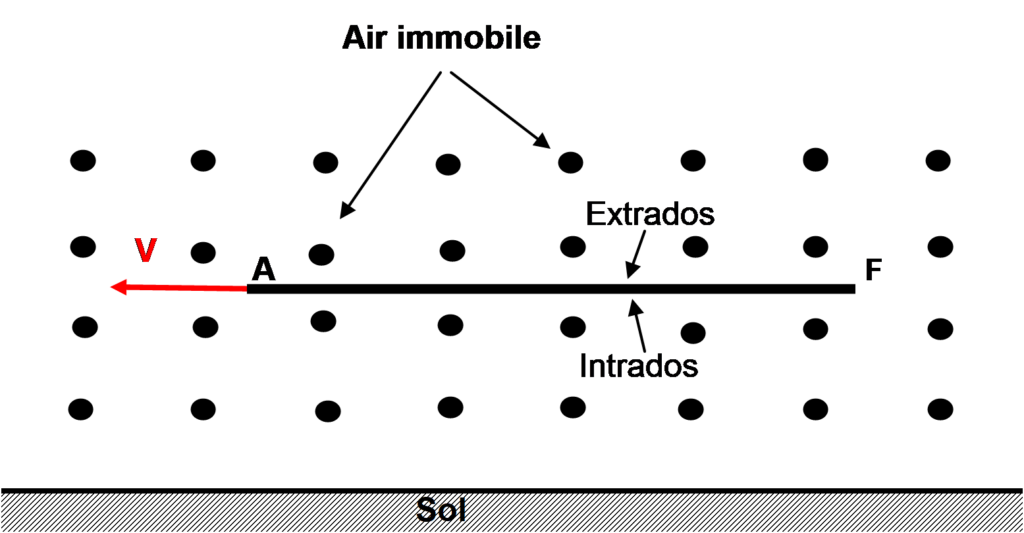

Avec une incidence non nulle: dans la figure 2 ci-dessus, la perception de 2 observateurs sera différente. L’observateur 2, positionné bien en avant ne constate aucun mouvement des particules d’air par rapport au sol. Ce que voit l’observateur 1 est différent.
Les particules d’air situées sous la plaque (en proximité immédiate de l’intrados), sont déplacées dans la même direction que celle-ci, avec une vitesse qui dépend de leur distance par rapport au bord d’attaque. On constate même qu’à un point (Aa) situé légèrement sous le bord d’attaque, la particule d’air au passage de la plaque se déplace instantanément avec la même vitesse.
Mais cette particule située en position 1 sur le schéma va quelques fractions de seconde plus tard se retrouver en position 2 et présenter une vitesse plus faible, puis en position 3, la vitesse d’entraînement diminuant au fur et à mesure que l’on se rapproche du bord de fuite.
La mise en vitesse n’affecte pas uniquement les particules situées en proximité immédiate de la surface, mais également celles situées plus loin de l’intrados. L’influence cependant diminue au fur et à mesure que l’on s’éloigne de la plaque
A l’avant de la plaque, l’air est soulevé et les particules contournent le bord d’attaque pour être évacuées du côté de l’extrados vers le bord de fuite. Les particules d’air se déplacent donc dans une direction opposée à celle du déplacement de la plaque. Leur vitesse est maximum au niveau du bord d’attaque et décroît au fur et à mesure qu’elles se déplacent vers le bord de fuite.
Le fait que la vitesse des particules est maximum au bord d’attaque est dû au fait que l’air doit contourner cette partie de la plaque, le rayon de courbure de la trajectoire étant très faible en raison de l’épaisseur négligeable de ce profil très particulier.
En se déplaçant, la plaque évacue donc de l’air par le dessus de celle-ci. Ce dernier est rejeté vers l’arrière.
Ce mouvement des particules est assimilable à une circulation, ici dans le sens horaire, des particules d’air autour de la plaque. Il faut être conscient que ce n’est pas la même particule d’air qui tourne autour de la plaque, mais un transfert d’énergie d’une particule à une autre qui génère ce mouvement d’ensemble.
A incidence = 0, la circulation est nulle. Elle apparaît dès que l’on crée une incidence et son intensité augmente avec l’incidence.
Apparition d’un champ de pression autour de la plaque en déplacement
C’est à travers l’existence de la circulation mentionnée ci-dessus qu’apparaît un champ de pression.
Le déplacement entraîne, quand la plaque passe de la position au temps T à la position au temps T+dT:
– une zone de surpression sur l’intrados,
– une zone de dépression instantanée sur l’extrados, mais surtout:
– une forte chute de pression sur l’extrados au voisinage du bord d’attaque, consécutive à l’augmentation de la vitesse lors du contournement par le flux montant. Ceci est la conséquence du principe de conservation de l’énergie.
Cette différence de pression entre l’extrados et l’intrados, appliquée sur la surface totale, génère la force de portance.
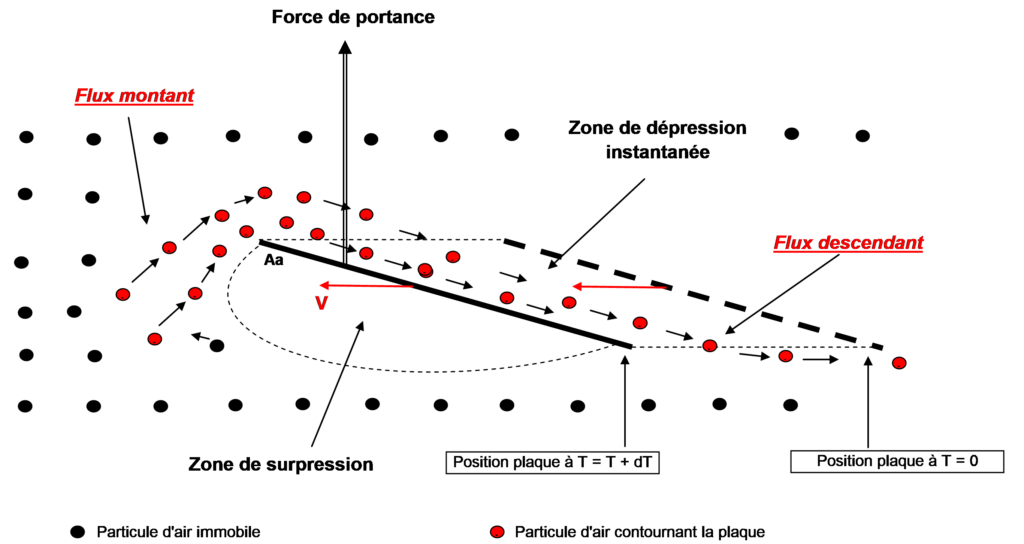
Quantification du champ de pression autour de la plaque / influence de la forme du profil
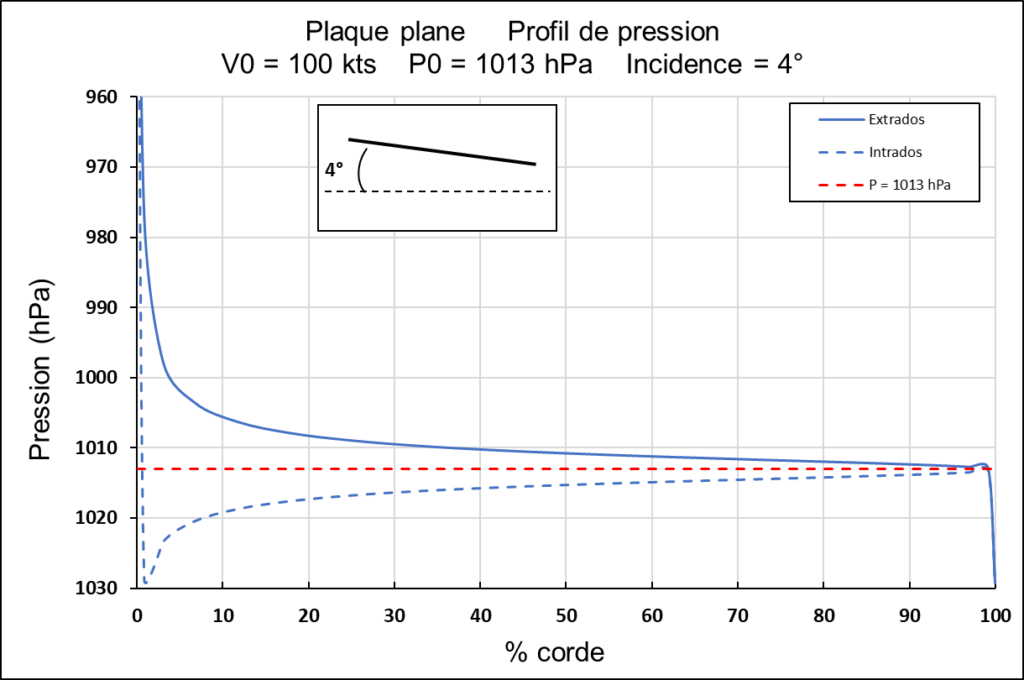
On considère un déplacement du profil, d’incidence 4°, avec les conditions suivantes: V0 = 100 kts, P0 = 1013 hPa. Les profils de pression sur l’intrados et l’extrados sont présentés en fonction de la distance par rapport au bord d’attaque, la longueur de la plaque étant prise à 100 %.
Plaque plane
On constate sur l’extrados une violente dépression dans le voisinage du bord d’attaque qui s’estompe très rapidement (= recompression d’extrados). Idem pour la surpression de l’intrados qui affecte essentiellement la zone proche du bord d’attaque et qui diminue rapidement vers le bord de fuite. Les coefficients de portance et de traînée obtenus sont les suivants:
Cz = 0.42 Cx = 0.03
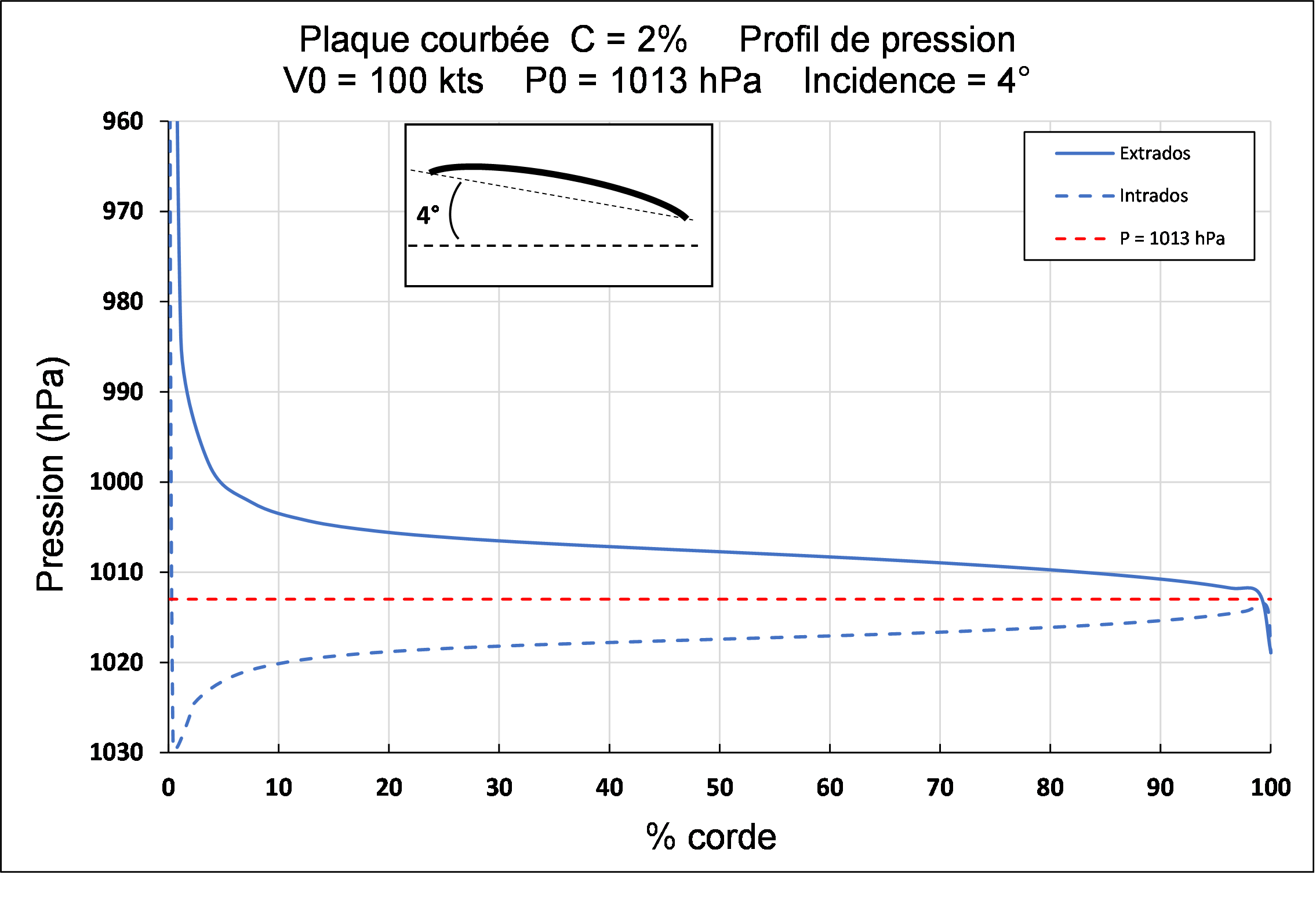
Plaque avec courbure de 2 %
Le pic de dépression sur l’extrados diminue légèrement (non perceptible sur ce graphique), celle-ci s’estompant un peu moins que pour la plaque plane. Idem pour l’intrados qui voit la zone de surpression légèrement plus forte. Les coefficients évoluent:
Cz = 0.65 Cx = 0.06
La courbure améliore nettement le coefficient de portance Cz mais le coefficient de traînée Cx augmente.
Profil d’aile NACA 2412 (courbure de 2 %)
On passe ici à un profil moins primaire que la plaque courbée, en créant un profil nettement plus performant, à savoir possédant, en plus de la courbure, une épaisseur et un bord d’attaque moins agressif que le bord de notre plaque (= profil dissymétrique).
Le pic de dépression sur l’extrados diminue drastiquement, et la zone de dépression s’est accrue. La zone de surpression d’intrados est moins prononcée, mais globalement les performances sont encore améliorées avec, en autres, une baisse notable du Cx consécutive à la forme globale du profil;
Cz = 0.73 Cx = 0.009
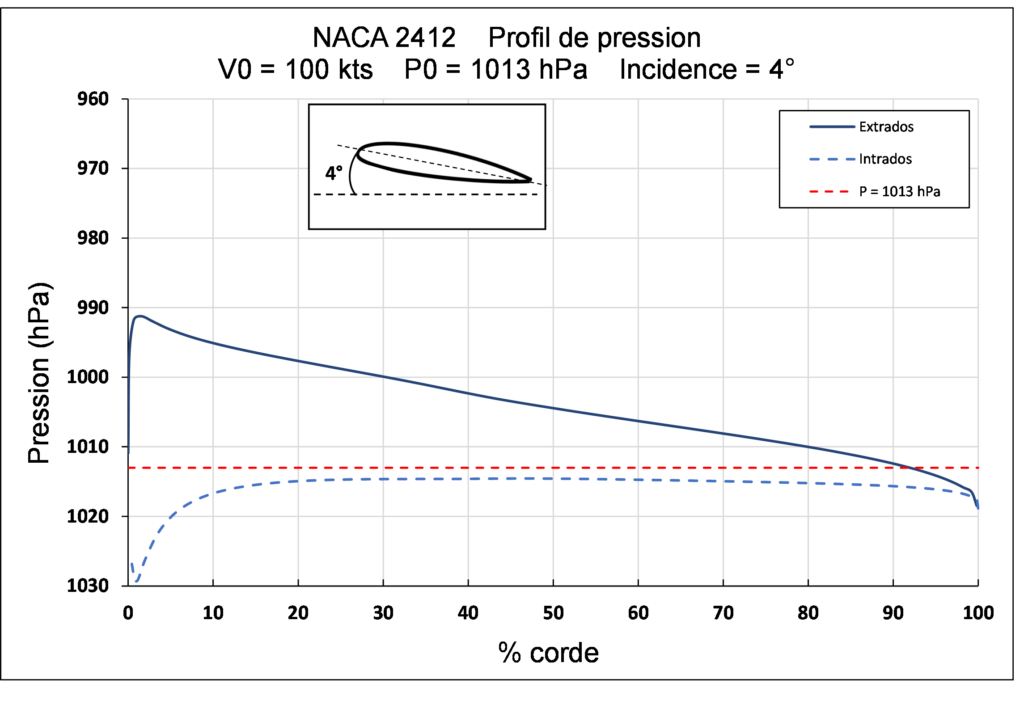
Notes:
- Pour de faibles incidences, un intrados convexe peut monter des zones de dépression. Dans le cas du NACA 2412, ces zones sont présentes en dessous de (environ) 2° d’incidence. Mais dans la mesure où la pression moyenne affectant l’extrados reste inférieure à la pression moyenne affectant l’intrados, on développe une portance.
- Ces profils dissymétriques possèdent une incidence de portance nulle qui est négative. On peut introduire la notion « d’incidence absolue » qui est l’incidence prise par rapport à cette incidence de portance nulle.
En résumé:
- La génération de la force de portance est la conséquence directe de l’incidence* du profil.
- La courbure de celui-ci et de façon générale la forme permet d’optimiser les performances.
(*) Certains puristes argumenterons que ce n’est pas l’incidence qui initie la portance puisque que celle-ci peut exister à incidence nulle si le profil est dissymétrique… Certes, mais dans beaucoup de cas, le Cz développé à incidence nulle est tel qu’il est difficile de générer à basse vitesse une portance satisfaisante pour compenser le poids de avion. Dans le cadre de l’initiation de l’élève – pilote, on peut sans aucun scrupule oublier ce point ou alors, se focaliser sur un profil symétrique qui, lui, montre un Cz nul à incidence nulle.
A télécharger:
- La documentation complète: Le phénomène de portance 1.6
Comment expliquer le phénomène de portance à l’élève-pilote…?
Il est évident que le niveau de détail de l’explication dépend des connaissances scientifiques de l’élève et de l’opportunité qu’il a pu avoir de poursuivre les études plus ou moins loin.
Comme indiqué plus haut, démarrer la présentation à partir du modèle « aile fixe dans une soufflerie » risque d’entraîner l’instructeur dans des explications qui, dans un souci justifié de vulgarisation, peuvent s’avérer imprécises voire inexactes.
L’exemple type d’une explication erronée est celle – bien connue car souvent entendue – qui consiste à avancer que l’origine de l’augmentation de la vitesse de l’air sur l’extrados est liée à la longueur de celui-ci. Le raisonnement est le suivant:
- « Deux particules d’air partant du même endroit en amont de l’aile, l’une passant du côté extrados et l’autre du côté intrados, doivent arriver ensemble au bord de fuite. Basé sur cette hypothèse, et puisque l’extrados est plus long que l’intrados, on annonce que la vitesse est plus grande sur l’extrados que sur l’intrados. Le rapport des vitesses est donc égal au rapport des longueurs ».
==> Partir du modèle: « aile en mouvement dans l’air » évite d’avancer cette ineptie.
Autres tentatives d’explications:
- « l’extrados, en raison de sa forme est assimilable à un venturi d’où la dépression ». C’est inexact. Une plaque plane génère une dépression sur l’extrados. Cela dit, on peut éventuellement assimiler le contournement du bord d’attaque par le flux montant à ce qui se passe dans un venturi, mais la forme de l’aile doit être laissée de côté.
- « L’aile applique une force sur l’air en le déviant vers le bas; par le phénomène d’action / réaction, l’air tire l’aile vers le haut ». Au niveau du bilan global, pour le système aile + air, ceci est exact et se réfère à la 3ème loi du mouvement établie par un certain Newton au 17ème siècle. Mais comme avec toute loi et son caractère généraliste, on reste sur sa faim concernant ce qui se passe en terme de pression sur l’intrados et l’extrados.
- « La déviation de l’air est due à l’effet Coanda sur l’extrados ». Ce phénomène existe dans tout écoulement de fluide sur des surfaces convexes, mais là aussi on explique pas l’intégralité du processus (en particulier le flux montant et la surpression d’intrados). Sans grand intérêt donc pour expliquer l’initiation du phénomène de portance.
==> Au final, l’élève doit garder en tête que l’origine de l’apparition d’une force de portance « aérodynamique » est la conséquence directe du déplacement de l’aile dans l’air (= dynamique) quand celle-ci présente une incidence.
Et ne focalisons pas uniquement sur le phénomène de dépression de l’extrados. L’intrados participe à la force de portance dont le pourcentage peut aller jusqu’à 25 % en fonction de sa convexité et de l’incidence du profil.
On peut schématiser le détail du processus comme suit. Les parties en rouge sont à expliciter plus ou moins selon les connaissances de l’élève.
