Décélération sur trajectoire rectiligne
Le but est ici l’évaluation théorique de la décélération et la variation de vitesse en fonction du temps Vi = f(t) dans les cas suivants :
- Décélération en palier suite à réduction totale de la puissance moteur
- Mise en palier suite à une trajectoire descendante sans modification de puissance (descente à puissance constante)
- Remise de gaz sur approche finale interrompue par une action initiale sur l’assiette
et ce, pour des masses différentes, à savoir 700 et 900 kg..
Rappel : équation de traînée (voir ici) X = ½ . ρ . V2 . Se + 2 . (m. g)2 / ρ . V2 . S . π. ƛ .e
Données utilisées : Se = 0,48 m2 ƛ.e = 4.3 ρ = 1,225 kg/m3
Situation 1 : décélération en palier par réduction totale de la puissance moteur
On suppose donc que la traction hélice devient nulle et seule la trainée subsiste ce qui va entrainer la décélération de l’avion.
On a alors : Γ = – X / m
Soit V0 la vitesse initiale de l’avion juste avant la réduction de puissance et X0 la traînée correspondante. La décélération initiale a donc pour valeur
Γ0 = – X0 / m
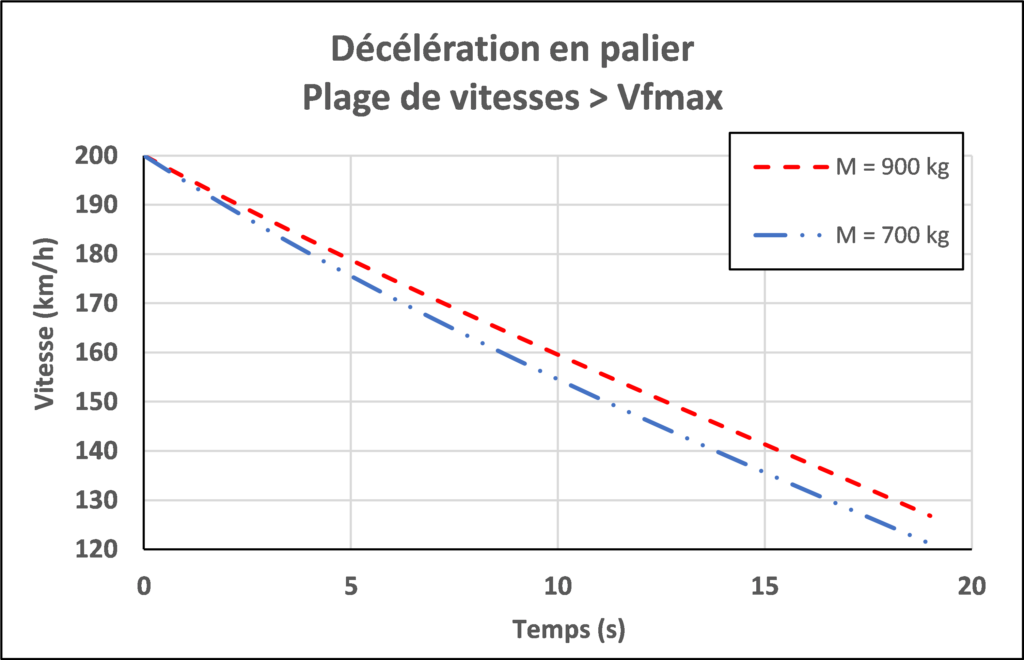
Cas 1 : la vitesse initiale V0 est supérieure à la vitesse de finesse maximum Vfmax
V0 = 200 km/h
Vfmax = 140 km/h (à 900 kg)
Vfmax = 125 km/h (à 700 kg)
Traînée initiale :
X0 = 1036 N pour M = 700 kg
X0 = 1125 N our M = 900 kg
La baisse de vitesse est moindre pour la masse de 900 kg.
→ L’avion décélère d’autant plus que sa masse est faible.
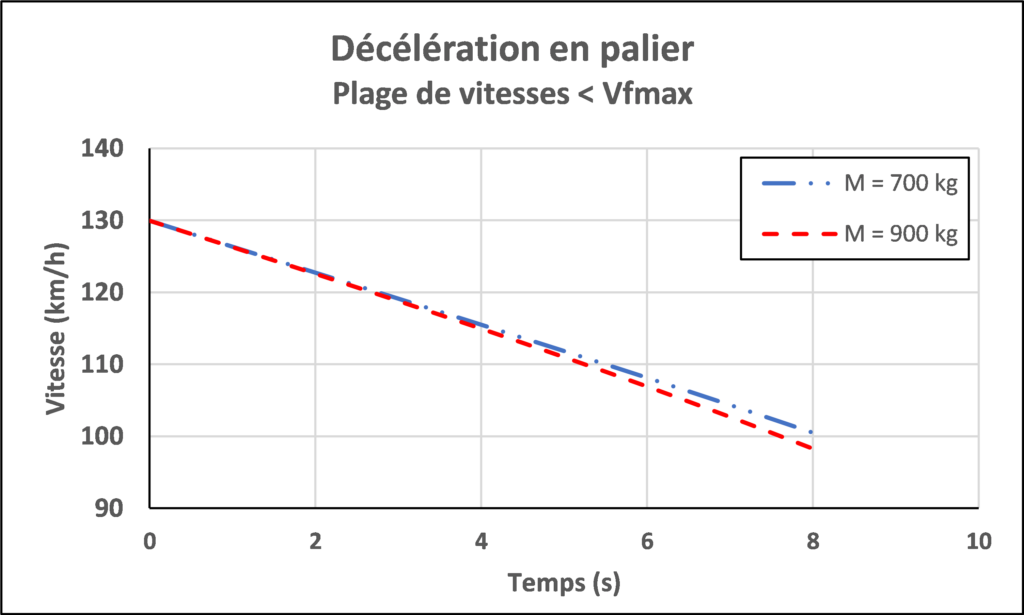
Cas 2 : la vitesse initiale V0 est inférieure à la vitesse de finesse maximum Vfmax
V0 = 130 km/h
Traînée initiale :
X0 = 703 N pour M = 700 kg
X0 = 914 N pour M = 900 kg
La baisse de vitesse est moindre pour la masse de 700 kg.
→ L’avion décélère d’autant plus que sa masse est forte.
Note : évolution de la décélération de part et d’autre de V fmax
La variation de vitesse en fonction du temps n’est pas linéaire contrairement à ce que l’apparence des courbes peut le laisser supposer.
La figure ci-contre représente la diminution de la vitesse ainsi que la valeur de la décélération Γ (qui représente la pente de la courbe de vitesse), pour une masse de 900 kg, entre 200 km/h et la vitesse de décrochage Vs (ici 95 km/h).
- Entre 200 km/h et la vitesse de finesse maximum Vfmax (ici de l’ordre de 140 km/h), la vitesse chute mais cette chute s’atténue avec le temps.
- Une fois passé Vfmax, la décélération s’accentue jusqu’à Vs.
La première partie de la décélération est la conséquence de la prépondérance de la traînée parasite, la seconde partie celle de la traînée induite.
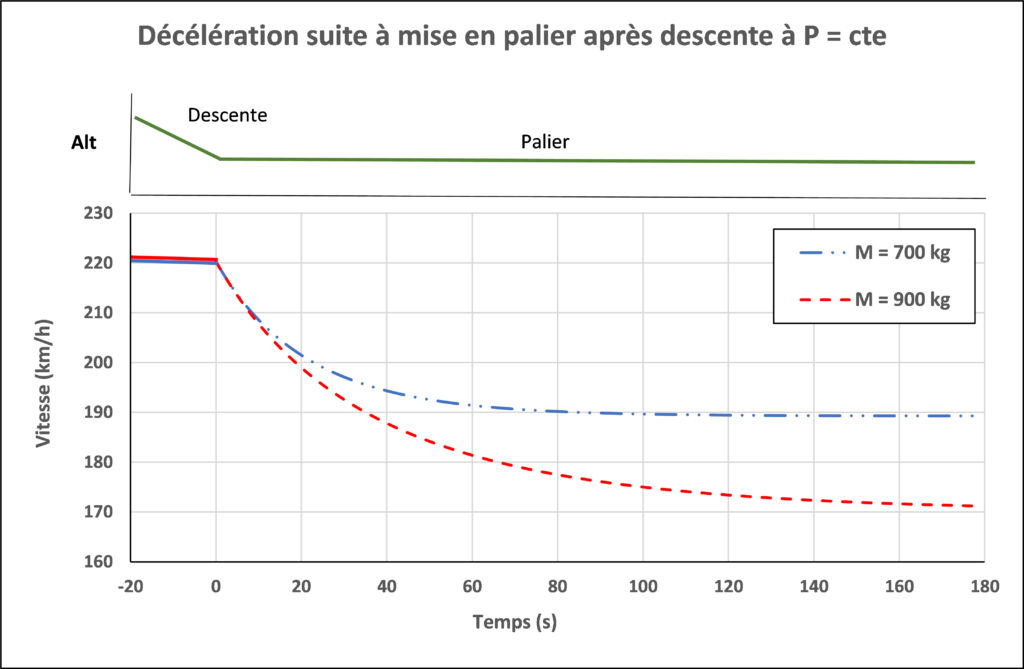
Situation 2 : Mise en palier suite à une trajectoire descendante à puissance constante
Pendant la descente, l’équilibre des forces est le suivant :
Traction totale (T) = Th + m.g.sin(γd) = X
Th : traction hélice γd : pente de la trajectoire.
A la mise en palier, la traction T se voit diminuée de m.g.sin(γd), T devient donc égale à Th , et donc inférieure à la traînée X. La décélération initiale a pour valeur :
Γ0 = (Th – X0) / m = – m.g.sin(γd) / m
Soit Γ = – g.sin(γd)
Exemple: avion en descente sur une pente de 2,4°
Vitesses sur trajectoire :
Vi = 220 km/h. Vz = – 500 pieds / mn.
Traînée initiale :
X0 = 1202 N pour M = 700 kg
X0 = 1275 N pour M = 900 kg
→ La vitesse finale après stabilisation est d’autant plus forte que la masse de d’avion est faible.
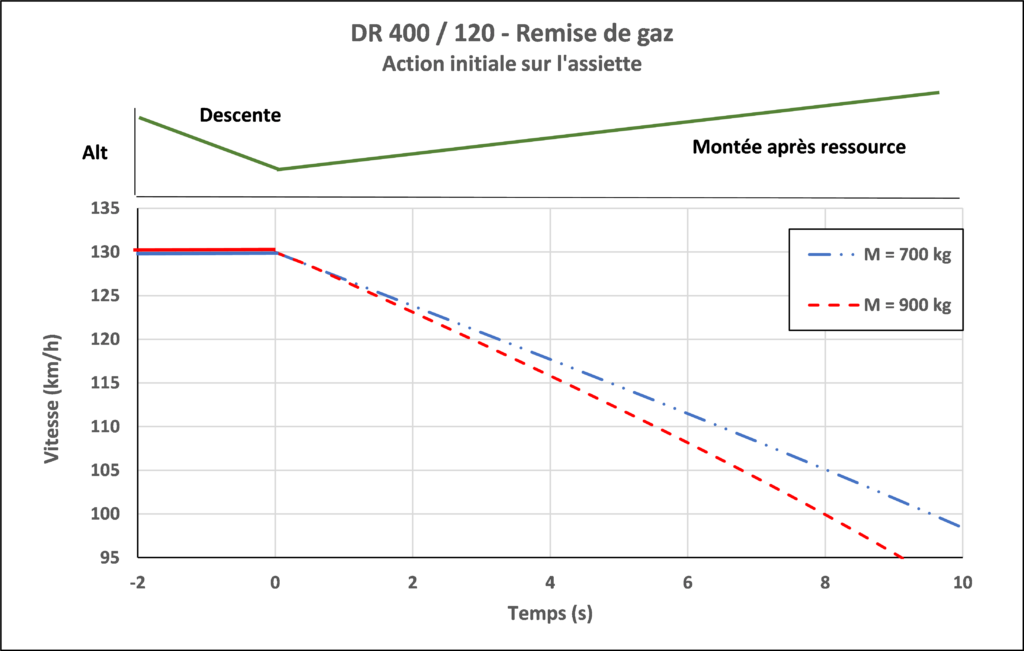
Situation 3 : remise de gaz sur approche interrompue en courte finale
On considère ici la séquence : action sur l’assiette puis remise de gaz. Sur la trajectoire d’approche finale, l’équilibre des forces est le suivant :
Traction totale (T) = Th + m.g.sin (γd) = X
Th : traction hélice γd : pente de la trajectoire d’approche finale
Immédiatement après la ressource et sur la trajectoire montante de pente γm :
- la traction T se voit diminuée de m.g.sin (γd) ; T devient donc égale à Th,
- la traînée initiale X0 se voit augmentée de m.g.sin (γm).
La décélération initiale a pour valeur :
Γ0 = – g.[sin (γd) + sin (γm)]
Exemple : avion en approche finale sur un plan de 3° (soit 5,2 %)
Vi = 130 km/h.
Après la ressource, prise d’assiette permettant une pente de montée de 2°.
Traînée initiale :
X0 = 703 N pour M = 700 kg
X0 = 914 N pour M = 900 kg
→ L’avion décélère d’autant plus que sa masse est forte.
